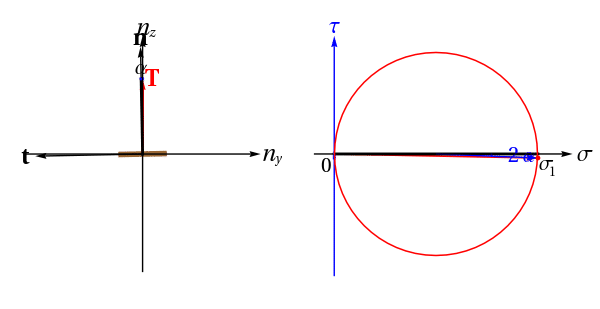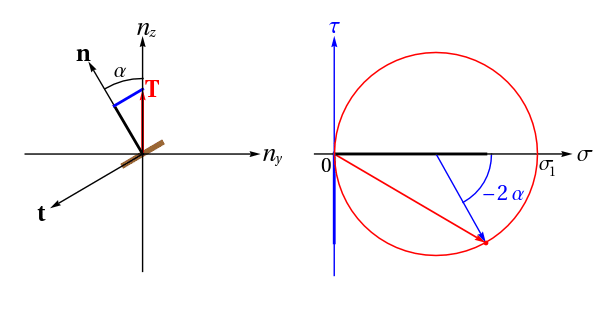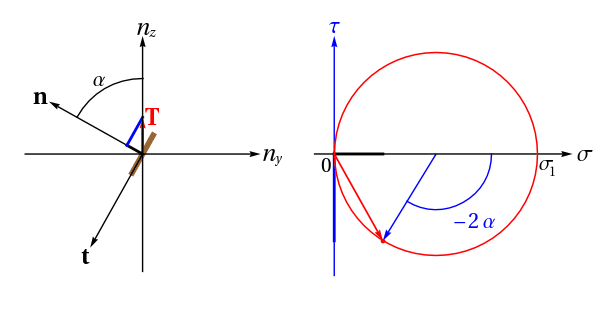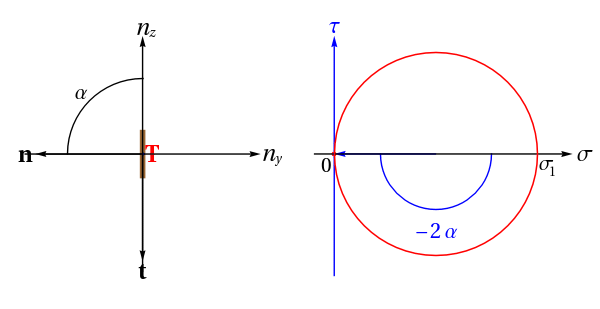
Par rapport au cas 3D, nous sommes maintenant dans le cas de contraintes planes, plus précisement, ici, dans le cas d'un essai de traction pure dans la direction z. La nouveauté est que l'on peut orienter le plan physique yz étudié, à gauche ci-dessous. On peut donc définir le vecteur tangent t faisant un angle de +π/2 avec n, la normale unitaire sortant de la coupe virtuelle représentée en marron. Lorsque n décrit un arc de cercle, on suit le vecteur contrainte T correspondant. Il est décomposé en sa composante normale algébrique σ (colinéaire à n) et sa composante tangentielle algébrique elle aussi τ (colinéaire à t).

      Droite : plan de Mohr (contrainte normale σ, contrainte tangentielle τ). Lorsque le vecteur n décrit un arc, le point représentatif rouge du vecteur T(n) décrit un arc du cercle de Mohr. Observez la « règle du -2α » sur les angles représentés. Ainsi, si on utilise un critère de Tresca, de contrainte tangentielle maximale, les directions de normale les plus sollicitées correspondront à -2α=±π/2 soit α=±π/4.

      Pour plus d'explications voyez l'exercice 3.1 du document de cours de mécanique.

      Contrarily to the 3D case, we are now in a state of plane stress, more precisely, here, in a tensile testing configuration (unaxial tension in the z direction). The thing is that we can now orient the physical plane, i.e. the yz plane, on the left on the figure above. We can therefore define, a virtual cut being given (the brown segment), not only its normal n but also its tangent vector t which is at an angle of +π/2 with respect to n. When n varies along a circle, we follow the stress vector T. It has a normal algebraic component σ parallel to n and a tangential algebraic component τ parallel to t.

      Right: Mohr's plane (normal stress σ, shear stress τ). When n describes a circle, the red point which represents the vector T(n) describes the Mohr's circle. Note the `-2α rule' on the angles. Thus, if one uses the Tresca criterion, of maximum shear stress, the most sollicited normal directions will correspond to -2α=±π/2 i.e. α=±π/4.