Kelvin-Helmholtz Instability
Mines Nancy - Department Energy - 2A

Kelvin-Helmholtz Instability in Fluid Mechanics

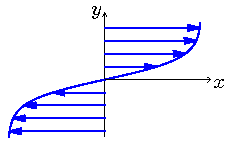
     In an extension of the problem 3.4 of the Lecture Notes, one may study the stability of a monophasic shear flow, without interface. The basic flow has the following profile:

With a numerical linear stability analysis, one observes a Kelvin-Helmholtz Instability. It is displayed below by the temporal evolution of streamlines and fluid particles (black disks) that sit, initially, on the line of maximum shear y=0, which is somehow the `interface' between the fluid flowing to the right (particles in magenta) and the fluid flowing to the left (particles in brown):

Thus, the small perturbation becomes a large perturbation !
The state obtained, when the instability has well developed, is a `vortex street':

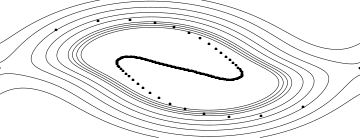
The `interface' between the fluid flowing to the right and the fluid flowing to the left has `rolled up' in the vortices. This `interface' may be, sometimes, visualized thanks to a cloud. That is, at least, what suggests the analogy between this computation and this photography by Brooks Martner, of the NOAA Environmental Technology Laboratory:

The computations have been performed with a spectral method. Some precisions and literature references can be found in the section 2.5 of this article published in 2008 in the Journal of Fluid Mechanics. Let us precise for instance that both the base flow and its normal modes are rotational, i.e., with a non-vanishing vorticity.
Please cite as follows:

PLAUT, E. Mécanique des Fluides 2. Mines Nancy Lecture 2018.

Animations realized with

Emmanuel Plaut
 Last modified: Tue Oct 20 18:38:45 CEST 2020